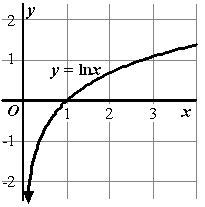Melodrama schreef:
ln(x) is voor de negatieve waarden voor x niet gedefinieerd in IR, dan krijg je met complexe getallen te maken
ik weet niets van complexe analyse af maar ik denk niet dat je dan simpelweg nog met afgeleiden zit eigenlijk??
Kirito schreef:
nee he, de helling zou dan tegengesteld zijnKirito schreef:
want zeg je nu niet eigenlijk dat de helling van ln(1) hetzelfde is als de helling van ln(-1) als de afgeleide [1/x] isKirito schreef:
oke miss lees ik het verkeerd
maar vgm klopt het nie
want in ln(x) kan de x alleen maar x>0 zijn
de afgeleide van ln(x) is dus 1/x als x>0, maar als je [1/x] zegt, zeg je ook dat alle getallen onder 0 ook een antwoord zouden hebben terwijl die dus niet gedefinieerd zijn omdat ln(x) die getallen uberhaupt neit kan uitrekenen? of lees ik dit echt compleet verkeerd
mijn brein gaat kapot ik heb al 3 maanden geen wiskunde meer gehadoke miss lees ik het verkeerd
maar vgm klopt het nie
want in ln(x) kan de x alleen maar x>0 zijn
de afgeleide van ln(x) is dus 1/x als x>0, maar als je [1/x] zegt, zeg je ook dat alle getallen onder 0 ook een antwoord zouden hebben terwijl die dus niet gedefinieerd zijn omdat ln(x) die getallen uberhaupt neit kan uitrekenen? of lees ik dit echt compleet verkeerd
ln(x) is voor de negatieve waarden voor x niet gedefinieerd in IR, dan krijg je met complexe getallen te maken
ik weet niets van complexe analyse af maar ik denk niet dat je dan simpelweg nog met afgeleiden zit eigenlijk??



 0
0 0
0 0
0 0
0 Om mee te kunnen praten op het forum dien je ingelogd te zijn.Nog geen account?
Om mee te kunnen praten op het forum dien je ingelogd te zijn.Nog geen account? 














 19
19